
C'est une lithographie que j'ai faite il y a deux ans, qui est en fait, à la fois, un hommage à Escher parce que sa structure est fondée sur une toile de Escher qui s'appelle Relativité, ça me permet de faire le lien avec la deuxième partie et puis comme vous voyez également apparaître des éléments astronomiques et surtout également les polyèdres réguliers dans le ciel, ça permet de faire la transition avec, donc, la deuxième partie de mon exposé qui va porter sur l'Espace élastique, c'est-à-dire une nouvelle conception de l'espace qui va se développer à partir du XXe siècle, avec la théorie de la relativité.
Alors avec cette théorie de la relativité on a réellement un changement radical de vision du monde en ce qui concerne la nature de l'espace et la nature du temps; suite aux travaux donc de Kepler, Galilée etc., c'est-à-dire à la naissance de la physique moderne, il y avait un premier couronnement de ces idées, avec la fameuse théorie de l'attraction universelle de Newton (1642-1727), qui propose un système du monde extrêmement performant, dirait-on aujourd'hui, c'est-à-dire qui permet d'expliquer par un système d'équation, et d'équations que nous avons tous appris à l'école, de façon extrêmement précise avec trajectoires des planètes, les interactions entre les corps, etc.; et donc, dans ce système newtonien, l'espace et le temps jouent le rôle de cadre fixé une fois pour toutes; l'espace et le temps sont des entités absolues, fixées à priori et à l'intérieur de cet espace et de ce temps donnés à priori évolue la matière selon les lois F = ma , l'action réaction etc. et lois de la gravitation universelle, par exemple.
Ce système prévaut jusqu'au début du XXe siècle, et puis, suite à un certain nombre de difficultés conceptuelles portant notamment sur la nature de la vitesse de la lumière etc., Einstein (1879) est amené à changer complètement cette conception, dans ce qu'on appelle la théorie de la relativité générale, où il va être obligé de considérer (tenir compte) notamment du fait que la vitesse de la lumière est un invariant absolu, au-delà duquel…qu'on ne peut pas dépasser. Einstein introduit de nouvelles structures, si vous voulez, qui s'appellent espace-temps-matière: c'est-à-dire une interaction subtile entre l'espace, le temps et la matière; c'est-à-dire séparément plus rien n'est absolu, l'espace n'est plus absolu, cela veut dire tout simplement que les mesures d'espace dépendent de la position et de la vitesse de celui qui mesure, donc l'espace est relatif au mouvement de l'observateur; les mesures de temps sont également relatives à l'observateur et, en fait, l'espace-temps a une certaine forme, a une certaine géométrie et cette géométrie est modelée par la matière qui est présente dans l'univers; donc on a une sorte de mariage subtil entre l'espace, le temps et la matière. Autrement dit, la force, notamment ce qu'on a appelé la force de gravitation, l'attraction universelle de Newton, qui était censé être une force émise par les astres massifs, par exemple le soleil qui retenait les planètes, qui les faisait tourner selon des orbites elliptiques n'est plus du tout considérée comme une force, mais comme un reflet, si vous voulez, d'une forme incurvé de l'espace et du temps, comme le reflet d'une nouvelle géométrie de l'espace-temps: donc c'est cette première équivalence entre la gravitation et la géométrie.
Et une deuxième équivalence entre maintenant la courbure de l'espace-temps va être en fait dictée par la façon dont les corps matériels sont répartis dans l'espace et dans le temps, ce sont les
fameuses équations d'Einstein, qui explicitent de façon technique cette équivalence entre géométrie et matière.
Alors, vous trouvez cela peut-être complètement abstrait et alors, pour essayer de rendre cela moins abstrait, je vais maintenant essayer de vous montrer ce que c'est que l'espace temps élastique: élastique parce que un espace temps déformé par la présence de matière.
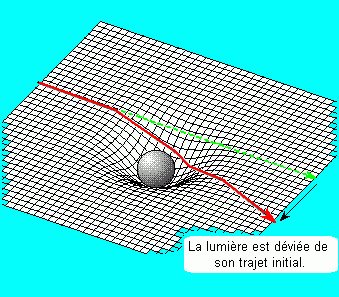
Je sors un morceau d’espace-temps qui est le suivant: évidemment pour le besoin de la démonstration je prends quelque chose à deux dimensions, je ne vais pas prendre un espace temps à quatre dimensions.
Alors imaginez un espace-temps réduit à deux dimensions.
Ce que vous voyez là c'est un petit morceau d’espace-temps. Vous voyez que les fils qui constituent la trame de ce filet sont rectilignes.
(Ils commencent à être un petit peu pas tout à fait rectilignes parce ça commence à être un petit peu fatigué, mais enfin normalement c'est rectiligne…)
Vous pouvez, en fait, imaginer que les fils rectilignes sont les trajectoires des rayons lumineux parce que, en fait, ce sont les rayons lumineux qui permettent de visualiser la forme incurvée de l’espace-temps. C’est un principe de base de la relativité générale. Les rayons lumineux sont à la base de tout. Donc, en l'absence de toute matière on dit que l’espace et le temps n’ont pas de structure particulière, ils sont plats, ils ne sont pas incurvés et donc effectivement les trajectoires des rayons lumineux sont rectilignes, on a un quadrillage bien régulier. Ce que nous apprend Einstein avec sa théorie de la relativité c’est que lorsqu’il y a de la matière, par exemple une étoile, dans le tissu élastique de l’espace-temps: eh bien le tissu élastique est incurvé au voisinage de l’étoile.
Ça veut dire qu'en fait ce sont les trajectoires des rayons lumineux qui sont déviées en frôlant une masse importante, par exemple en frôlant le soleil. Mais en fait c’est la forme même de l’espace et du temps qui est incurvée; autrement dit, les rayons lumineux continuent à aller en ligne droite, mais en ligne droite dans un espace courbe. On appelle cela des géodésiques: en mathématiques, les courbes qui permettent d’aller d’un point à un autre et qui sont de longueur minimale.

Donc on a des géodésiques dans un espace courbe. Et alors, si vous voulez, par exemple, les trajectoires des planètes dans ce schéma-là, ne s’interprètent plus, je vous dis, avec une force d’attraction qui émanerait de l’objet central, les (trajectoires des) planètes sont considérées, par exemple, comme des corps totalement libres, c'est-à-dire soumis à aucune force, et qui circulent librement sur ce tissu, mais comme le tissu est incurvé et bien parmi les trajectoires possibles d’une particule soumise à aucune force, il y a notamment les ellipses qui tournent autour de ce creux. Et donc c’est ainsi l'idée de base de la relativité générale. Alors bien évidemment la déformation du tissu élastique de l’espace-temps est d’autant plus importante que la masse que vous mettez est plus importante; donc voici la déformation beaucoup plus grande qui serait causée par un astre, par exemple, beaucoup plus massif et beaucoup plus dense que le soleil.
